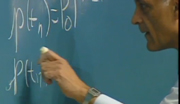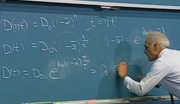Leslie Kaelbling: 6.01 Lecture 10

PROFESSOR LESLIE KAELBLING: OK, so what have we been doing? The last two weeks or so, we've been thinking about probabilistic state estimation. So the idea has been, imagine that there's some system out there, and you're not sure what state it's in. But you can kind of poke it by doing things to it. You can give it inputs, and you can see what outputs it generates. And you're trying to estimate the internal state.

So in state estimation, you can think of the problem as having this machine with some internal, hidden state that you don't really know, right? And what you can do is generate inputs-- which we also sometimes think of as actions-- and we can see what the outputs are.

And what we've been trying to do is estimate a probability distribution on the hidden state. So that's what we've been thinking about. And we've been thinking about, well, maybe this system is a robot wandering around in the world, and we're not sure where it is. Or it's a copy machine, and we're not sure how well it's working, and so on.

So this is an estimation problem, right? We're not really trying to change the world. We're not really trying to change this machine. We're not thinking about whether it's a good state or a bad state. There's none of that. It's just about looking at the thing and trying to understand, well, what state do we think it's in?

OK, so what we're going to do now-- today and next time-- is talk about another problem that we might have with respect to systems like this, which is really the control problem. So when we thought about trying to get the robot to go down the hallway, we were thinking about a plant, right? So we had a plant. And we were interested in giving it some inputs. And we wanted to see what it outputs.

And in the case of the control system stuff that we did, we assumed that in fact, the state of the plant was observable, right? That is, when the robot was going down the hallway, we could perceive its distance to the hallway. Although, sometimes we had a sensor that made it be delayed by one, right?

But let's just imagine for right now that we can observe the state of the system, right? So we developed LTI controllers, which we could hook up to the plant, that would observe the state and generate a new i so that the plant would go to some state that we liked.

And we found that we could do that. If everything was linear, we could effectively just, in some sense, solve for a good controller, right? Maybe we had to do some more complicated design. We had to think about whether it needed to have some extra delays and so on. But we looked at the design problem.

So now what we're going to do is think about this same problem, really-- the problem of being given a system, which, given some inputs, has an internal state. And the internal state changes in a way that depends on the inputs. And we're going to have some desired states. What we're going to look at now-- the general problem where the dynamics of this machine are not necessarily linear, right?

So when we did this in the LTI systems case, we considered, how do we solve this problem? How do we think about solving this problem? How do we build a controller for the case where the states are linear?

Here, we're going to assume that the dynamics, the process that describes how a new state depends on a previous state, is arbitrary. It can be anything, right? In our state machine way of describing things, we have this getNextValues, right? If we have a machine dot getNextValues, it takes a state and an input and it gives us a nextState and an output. And it can be any computer program in the whole world that takes a state and input and gives us a nextState and an output.

So what we're going to do now is think about, if you give me the description of a plant, a system in the world that you want to control-- which is deterministic, right? So in the scope of this class, we're not going to worry about how to control a probabilistic state machine. That's a thing you can do, but we're not going to do that.

So we're just going to assume that we have a plant, and it's deterministic. So if you give me a state and an input, I can tell you what the nextState is going to be. And what we're going to do is try to figure out, given a description of how this machine works, and given a desired ending state, or set of ending states-- we're going to try to figure out, what is the sequence of inputs that you can feed this thing so that it goes into the state you want?

OK, so that's all very abstract. Imagine that this is a description of how the robot moves in the world. If I tell it, move forward one meter, it moves forward one meter. If I tell it, move right one meter, it moves right one meter. So you can imagine some description of a robot like that that's quite discrete in moving forward and backward and so on. Maybe there's obstacles in its way.

Then this problem is what we'll call a planning problem. It's a problem of finding a sequence of inputs-- like, go forward, forward, left, left, forward, left, left, right, forward, whatever-- so that it arrives in a place that we want it to go.

So just so you understand these two pieces, here we used a model, a description of how the world worked, in order to try to estimate what was going on in the hidden internal parts of the system. Here we're going to assume we have a system. And for now, we're also going to assume that we know the state of the system, and we know that it's going to transition deterministically.

Knowing that, we're going to try to figure out a sequence of inputs that we can feed to this thing so that it arrives in the state we want it to go to, OK? Does that make sense to everybody as a problem? So what sequence of inputs will drive this thing into a state we like? Yep.

STUDENT: How did you get from the probabilistic state estimation to the deterministic?

PROFESSOR LESLIE KAELBLING: Yeah, OK, good-- so basically, what we're showing you is two pieces of a harder problem, which is way cool, but we can't quite get there, right? So in our dreams, and in real life, what we have is a system which is probabilistic where we can't really know the internal state, and where the dynamics aren't really deterministic.

And we have to think about how to control that thing. And that's pretty hard, right? Because what we have to do is do estimation to get a belief about what's going on. And then we have to base our actions on the belief, right? So saying, oh, gosh, I don't know where the robot really is. I think it might be here, or it might be there. Now what should we tell it to do?

So that's a really cool and interesting and a hard problem. We have to understand this deterministic version of it first so we can work our way up to that. In this class, we won't quite work our way up to that. That's a great question. OK, does that make sense to everybody?

OK, so our problem for today is going to be planning-- so finding a good sequence of inputs to drive a machine into a state that we like. That's the goal. So here's the AI world's favorite stupid planning problem. Probably everybody's done this-- this silly little puzzle with the sliding tiles. Maybe it has pictures of a dolphin on it instead of the numbers one, two, three, but it's got something.

And you can slide the tiles around. And they're in one arrangement here, and you'd like them to be in a different arrangement. And it's a puzzle to figure out what order of moves you can make in order to go from this state to that state, right? And look, there's the answer-- right, good-- 22 moves. There's some answer.

So if I gave you one of these things, you would mess around with it for awhile-- some longer than others. Some of us would lose patience and throw the thing across the room. But maybe eventually you would solve the problem and we could ask the question, well, how many moves did it take you to solve the problem? And we might want to know, how hard a problem is this? Was that the optimal strategy for solving it?

So one thing to think about is, how hard a problem is this? How hard is it to figure out the sequence of moves that you can make to get this thing from one state into another, right?

So first of all, I just want to be sure that you can see this problem as a state machine. That this crazy little piece of plastic with the slidey tiles-- it's a kind of a plant, right? It's a thing that you can do things to and change its state. And we can say, we want its state to be this, so what sequence of operations can we do it in order to get it from this state to that state?

All right, so there's this question about-- how many board configurations are there? We can just talk through this, right? So there's nine squares. There's nine possibilities for the first square, nine different values that you can have in there. Because there could be a one, a two, a three, a four, a five, a six, a seven, an eight, or blank space. Having decided what's going to be in the first square, then there's only eight possibilities for the second one, and so on. So you can do this big multiplication and get 9 factorial states.

OK, there's 9 factorial states. Now, 9 factorial states-- so that seems like it's a pretty big problem. And then, we might also have to think about how many paths there are through the space. So anyway, it's a tricky thing searching through this space of possible configurations of this thing.

And we would hope that we wouldn't have to look at all the configurations, or even all the orderings of all the configurations, in order to find a good strategy. So we're going to take this opportunity both to think about a problem of finding a sequence of controls for a plant-- thinking of that as a state machine and a control problem. It's also an opportunity to get an introduction to the way computer scientists think about algorithms for solving problems. So it's another thing that we're going to do while we're working on this.

OK, so what we want to do is study what's called a search algorithm. So a search algorithm takes a formal description of a problem. And it will do it in terms of a state machine, ultimately, because that's how we like to describe these kinds of systems. And it's going to somehow take that description and see if it can find a sequence of inputs that will go from the starting state to a goal state that we like.

And we're going to be interested, for instance, in trying to find a good solution-- so one that minimizes the length of the path, for today. And we would also like to find an algorithm that runs sort of fast. Because the problem looks kind of big and kind of hard, and it seems like if we enumerated all the states or all the orderings of all the states, that would not be probably a good way to address the problem. So we want to try to be clever in how we organize the computation so that we can find a solution quickly.

OK, so instead of that puzzle, let's look at a much smaller problem. So here's a problem. It's like a tiny version of the Google Maps problem where we have nine cities. So just imagine that these are now-- this is just a path-finding problem. So the robot can walk around in this graph-- or you can, or somebody can, walk around in this graph-- and we're going to want to go from one state to another state in this grid.

So in this system, the states are the locations-- we'll just do this. The states are A, B, C, D, E, F, G, H, I-- that's where the robot can be in this world. And the actions it can take are to move to one of the states that it's connected to by a red arc, right? So for instance, if we want it to go to I, one path might be east, south, south, east. That would be an example of a sequence of inputs that we give this thing that would take it to where it needs to go.

OK, so one way to think about finding a path through a domain like this is to make what we call a search tree. So here's a search tree. Now, so this is a search tree that assumes that we're going to start at location A. If we're going to start at a different location, a different state, we would have a different search tree, which had a different root, a different node at the top, a different state label here at the top.

So this search tree has lines and circles. The circles in the search tree are labeled with the names of states. But they are not equivalent to states. I'll show you what I mean by that in a minute. So here is what we'll call a node. So with these circles in the search tree, they look like the circles in this graph, but they're really in some sense a different kind of circle. Probably we should have used squares.

OK, so it's labeled with a state. So we say, well, what we're going to do is we're going to start at state A. Now, from state A, we have a choice of what we're going to do. We could go along one of the arcs that we're connected to and get to state B, or we could go along a different one and get to state D, right? So from A, we can get to B or to D.

So we have a choice about what to do. And then, if we go to B, we've got three choices, right? Because B is connected up to three different neighbors. So from B, we could go back to A if we wanted to, or we could go to C, or we could go to E. And if we went to C, from C we could go to B or to F and so on.

So this is a tree that shows us all paths of length three in this map, OK? Does that make sense-- that this is a tree of paths? There's only nine states here, but already, of length three, we've got-- two, four, six, eight, 10, 12, 14-- 16 paths.

So there's an A here and an A here and an A up here. These different nodes, they don't really stand for-- they are labeled with states, but they stand for partial paths through the map, right? So this A, this search node A, stands for the path that goes ABA.

That's a path in the world. It's a thing you could do. It's probably not a smart thing if you're trying to get somewhere efficiently, but it's a thing you could do, right? You could go from A to B to A. Similarly, this A here stands for A to D to A. This B down here, it stands for A, D, E, B, right-- ADEB.

OK, so in this tree-- this is what we'll call a search tree. The search tree has nodes. The nodes in the search tree stand for paths through the domain-- partial paths. Is that clear? It's really important to understand the distinction between the nodes in this thing and the nodes in this thing, right? These are paths. These are states, places you could be. These are sequences of actions that you could take and sequences of states you could go through.

OK, so now, I always-- when I'm faced with a computational problem, my favorite thing to do is-- and because I'm lazy, maybe-- is to think of the stupidest possible algorithm. It's always the first thing you should do if you're given a computational problem. OK, we know in our head we want to be efficient and stuff. But anyway, start with the stupidest possible algorithm. So what would be the stupidest possible algorithm for finding a path through this environment, let's say from A to I? Anybody, give me a candidate, stupid-- yeah?

STUDENT: Generate a random sequence of steps and then see if that sequence satisfies your--

PROFESSOR LESLIE KAELBLING: OK, that's a good one. Generate a random sequence of steps and see if that's the answer. That's lovely. So that's an example of a style of algorithm called generate and test, or a sampling algorithm. Even stupider-- if we're going to be stupid, let's try to be really stupid. Even stupider, we could say, well, let's just generate all the paths, and then look through them to see if one of them is our answer.

So that's even less clever than the suggested example, right? So we could say, all right, we'll generate all the paths, and then we'll look through them and see if we can find one that gets us where we want to go.

Well, OK, but the tree, as we've discussed it here, could be infinite, right? Because I've got this thing going, for instance-- A to B to A to B to A to B to A to B. And that could go on forever. And that's going to get us where we want to go. So generating all the paths isn't a good idea.

So what we're going to do is actually arrange it so that we somehow incrementally build this tree. We can't build it all at once and then go looking in it. So even though we talk about the search tree as an object, it's kind of an abstract object. We'll write a computer program that constructs some parts of this tree. But we're not going to ever-- it's inconceivable, [FRENCH], to generate the whole thing.

OK, so representing stuff in Python-- I'm going to leave that out for now. Yeah-- well, no. OK, here we go. So let me just point out a couple things here of how we can represent this problem in Python. So what we've done is, the important things are the three things down here. So first of all, there's an initial state. An initial state can be anything you it to be in Python. It could be a list of-- a tuple, it would need to be a tuple of things. In this case, it's just a simple name of a state-- A.

And we're going to have something called the goalTest. A goalTest is a procedure that takes as input a state and tells us if it's a good place to stop. Now, you might wonder why we have to be so indirect about it. If I say, I want to find a path from A to I-- what I've said here is, well, I'm going to say that I'm trying to find a path from A to I by saying that I have this test on states. And I'm going to return True if my state is I. So that's what it means to have I as a goal.

So that's about getting from A to I. And in my GPS, I can tell it that I want to go to a particular address, and then it'll find a path from A to I. But I can also tell it that I want to go to the nearest Starbucks, for instance. I've done that. And so in that case, the goalTest doesn't say, I need to go to a particular place. It says, well, if you give me a state, I'll look at it to see if it's a Starbucks. And if it is, I'll say, yes.

So there's going to be more than one state that would be satisfactory in that case. So we want to be able to have multiple possible good places that we end up.

So we have a way of saying the initial state. We have a way of saying what it means to be happy with the place that we're ending up. And then we're going to have to have some kind of a procedure-- which is basically getNextValues without that second part-- which says, if I have a state and an action, I want to return the nextState.

And what's encoded in this example-- I'm not going to go through it in detail-- is just using a dictionary to describe the connectivity of this particular example, right? So from state A, we can go to B or D. From B, we can go to A, C, or E, and so on. So this is just a dictionary way of describing which states are connected to which other states.

And we're just using integers as the actions, right? And they're just-- pick which of the neighbors we're going to go to. So that's a simple way of describing this particular connectivity.

OK, so now, in Python, we have to be able to describe a tree. We're going to build a part of a search tree. We're not going to build the whole thing, but we're going to build a piece of it incrementally.

And what we're going to do is we're going to hope to just build bits and pieces of it until we can get to a good path that satisfies the requirement that it starts at the starting state, it ends in a state for which the goalTest is true, and that each nextState in the path is one that would have been generated by getNextValues. So those are the requirements.

In Python, we'll have a class to represent a node in a search tree. And the important things about this class-- what they remember. So each node-- say, this node here. This is a node in the search tree. It remembers the action that was taken to get there. So in this case, it's action one.

It remembers the state in that node-- in this case, it's E. And it remembers its parent. And its parent is the search node up here, right? So if you know your state, and the action that you got to get there, and your parent, then you could, for instance, reconstruct the path all the way from yourself up to the start state by saying, well, if you ask me a path to me, if I'm the root, then I just say-- right, if I don't have a parent, then I can tell you the path. It's just me.

If I do have a parent, then I ask my parent for its path. We say, hey, how do you get from the starting state to the parent? And then you can just add my action and my state onto the end.

So a search node is a way of encoding a path in the tree by saying, well, I have a parent. And then, to get to me from my parent, you just need an action and the state name.

All right, so now, what we're going to think about is a way of incrementally building up the search tree so that it starts in the start state, gets to a goal state, and respects the dynamics of the domain. And the way that we're going to do that-- and it's sort of like how you might think of searching this way.

Actually, I think people probably mostly don't. But while you're thinking about how to get from here to some place on campus, you could imagine thinking about some sense of partial paths, some partial solutions, that you might have in your head in play. And you might ask yourself the question, well, here's a partial solution. Can I improve it in some way? And then, that might give you some new partial solutions, and so on.

So what we're going to do is work with a list, or sort of a set, of partial solutions. That's going to be how our algorithm is organized. And that set of partial solutions is going to be called the agenda. Those are the things we have to work on.

So what's going to be in the agenda are nodes in the search tree. And the way the algorithm is going to work is it's going to pull a node out of the agenda, typically ask if it's the goal-- if it is, yay, we're done. If not, it's going to take the children of that node-- those places that we can get to in one step, those are its children-- and put those in the agenda. And it's going to do it until the agenda is empty, in which case it means that it's unreachable-- you couldn't get to a goal state from the starting state-- or we hit the goal. Or we hit a goal.

So let's try to do this a little more concretely. We'll look at it in Python. This will still be a little bit abstract, and then we'll make it completely concrete.

So we're going to define a procedure search, which takes an initial state-- we already saw what an initial state might be; a goalTest, which is a procedure which looks at a state and tells you true or false; a set of possible actions that you could take; and the successor function, which is basically getNextValues, which says, if you're in this state, and you take this action, where do you end up?

All right, so to start out, it turns out that this little if statement was something I didn't have in my code for a while. And it would generate totally random, stupid answers sometimes, and I could never figure out why. This is the thing that the optimist has to do. If it turns out-- if somebody happens to call the search procedure saying, please find a Starbucks, while your parked in a Starbucks parking lot, it should just return right away and say, you're there already.

OK, so these are the kinds of things that are easy to forget, but it's the basic base case in some sense of this problem. So if the initial state of this problem satisfies the goal, then you can just return right away. And what do we return? We return an action and a state. We return a path. A path is a list of action-state pairs.

So we say, well, with no actions at all, you can be in initial state. And that's where you wanted to be, so good, we're done. All right, if that's not true, if it doesn't happen that we're already in a place we need to be, then we're going to put a search node in our agenda, and then we're going to start the searching algorithm.

And remember, a node contains an action, a state, and a parent. It didn't take us any actions to get here, because we're here right now. So that's None. The state is the initial state, and we have no parent. This is the root node, which is an orphan.

OK, so now, all of our search algorithms are going to have this character. And it's going to seem abstract. And we're going to do a bunch of cartoons in just a minute, so hang tight. OK, so this is now the meat of the search algorithm. It says, well, the agenda is not empty. And I've written in blue here things that we don't really know how to compute yet, but we have ideas for.

So if the agenda's not empty, that means that we still have some options. We still have some ideas about how we might find our way to a goal. Then, what we're going to do is, we're going to consider all the possible actions that we can take. And we're going to say, well, if I were in the state of the search node that I'm trying to expand, and I were to take action A, what would my new state be? Where can I get to from here?

And I make a new search node that says, well, by taking action A, I get to this new state, newS, and parent was my parent. Then, I check to see if the state that I just discovered was a goal. And if it is, I return it. And otherwise, I take this new search node and put it back in the agenda.

OK, mystifying-- let's do it now a bunch of times for a bunch of different versions of that algorithm. Let me say that I was purposely-- I was sort of coy here in this code. I didn't say how we're going to get an element out of the agenda, and I didn't say how we're going to add a new node back into the agenda. And it's going to turn out that different choices for how to do this will generate really different behaviors of the algorithm.

OK, now, let's see if we can simulate one of those algorithms on this graph. So we're going to take the following version of that algorithm that says, my fundamental operation is to take the first element out of the agenda and replace it by its children. OK, that's going to be how this algorithm works in searching for paths.

So I start out, and I put in the agenda a path which consists of this one node, A. That's how it's initialized. Now I say, OK, I'm going to replace the first node in the agenda-- so I've colored that A, that guy up at the top-- we're going to replace it. And we're going to replace it by its children. Because we test to see, is A the goal? A is not the goal. So we don't stop. We have to keep going.

So we're going to replace the node A by its two children. The children of A are the nodes AB and AD, OK? Note that to name a node I have to describe it with a path. The state is not the same as a node. And we'll use paths to name the nodes in the tree, right?

So the agenda was A. I took A out, and I replaced it with its children-- AB and AD. OK, now, I'm going to take out the first node from the agenda, which was AB, this node, and I'm going to replace it with its children-- ABA, ABC, and ABE. OK, what's the next step going to be? Who am I going to take out? ABA. And what am I going to replace it with?

STUDENT: ABAB.

PROFESSOR LESLIE KAELBLING: ABAB. Right, so ABA is the first one on the agenda. I'm going to take it out. That's like saying, ABA. I'm going to take that guy out, and I'm going to replace it with its children. So I put in ABAB and ABAD.

OK, how do you think this thing is going to explore the tree, just sort of intuitively? What's it going to do?

STUDENT: Always take the left side.

PROFESSOR LESLIE KAELBLING: It's going to always go down the left-most branch, right? And in a domain like this, if we don't do something about it, you can see that it's just going to spend a lot of time doing what, in particular?

STUDENT: ABABAB--

PROFESSOR LESLIE KAELBLING: ABABABABAB, right? It's like saying, oh, I'm always going to take left turns. I really like left turns. Good, go left turn. I'm just going to keep considering left turns. OK, that is not a good way to find your way through a map. So this is not going to be our ultimate solution to the problem. But it's going to help us see how making different choices ends up in different results.

OK, did this little simulation I did make sense to everybody? Please ask if not. OK, so this process, digging down ever deeper, is called depth-first search. And It looks really stupid right now. We'll fix it up so that it's not so stupid in a little bit.

OK, let's see what other choices we could do. We could decide that what we want to do is replace the last node in the agenda by its children. I'm just going to simulate this real quickly.

If we do always replace the last node by its children and put the children on the end, we get exactly the same sort of behavior, only now it always turns right instead of left. I don't know, anyway, it's going to go around in some other way that's not so good. So that's a kind of dept-first search.

All right, now let's look at something that's really pretty different. So what we're going to do is change the rule. We're going to change the rule so that what we do is take the first node off of the agenda, and we take its children as before, but we put its children at the end of the agenda, at the other side.

So let me show you how this works out. We start with A, as before, expand it, put its children in the agenda-- nothing really changes. Now, we're going to take AB out and put its children in. But instead of putting its children at the front of the list, we're putting its children at the back of the list.

OK, that hasn't actually changed anything yet, but it's about to. Because if I'm doing depth-first search, the next node that I would expand would be ABA, right? I would go look at the children of ABA. But my agenda has a different order. It has AD here up in the front. So what it's going to do next is take out AD and put in the children of AD-- so I've got ADA, ADE, ADG.

So what's interesting about that? What's the pattern we have right at this moment? Somebody says, like this. OK, I get that. I think I want to channel now that person who was going like this, and suggest that, perhaps, what you meant to say was that we're actually going to go through this tree in ranks, right?

First, somehow we looked at all the paths of length zero, and then all the paths of length one. And now, look-- we have all the paths of length two in our agenda. And you can believe-- we'll watch it in just a minute-- that we'll probably get all the paths of length four next, right?

So what I do now, I take off the first guy-- ABA, that was this one-- and I generate its children-- ABD, ABB, ABAB, and ABAD. But I put them at the end. I say, oh yeah, you guys, I'll get to you later. Not right away-- later.

So by putting these guys off, what node am I going to expand next? This C right here, right? And then I'll put in its children. And then I'll expand E, and I'll put in his children, and so on. So I'm going to have an algorithm that has this property of going along rank by rank, depth by depth.

This is called breadth-first search, right? It searches broadly-- all the paths of length one, all the paths of length two, all the paths of length three. But what's interesting is that we only had to change a simple thing in the way our algorithm worked in order to get that really pretty difference. I mean, a simple thing in the definition gave us a fairly large difference in the behavior from depth-first to breadth-first.

OK, so how do you make that come out in code? How would we write a Python program to do that? Well, there are these nice ideas-- again from the study of data structures-- that let us build these algorithms very compactly and nicely. So there are two things. There's something called a stack and something called a queue. And let's just expand those by example here for a minute.

A stack, the common way that people think about it-- of course, I don't think they have these anymore. Back in the good old days, or perhaps the bad old days, before everybody's food came in a Styrofoam container-- but maybe in the dorms they still have these things.

Anyway, in a cafeteria, there were these stacks of plates with a spring underneath them. So you'd put all these plates in there. And you'd take out the top plate, and the other ones would rise up. You take off another one and the other ones would rise up. So that's a stack.

OK, so what does that mean? If I put something in it, it goes down to the bottom. And then, if I put something on top, I'm going to get the top thing back out when I get it out.

All right, so let's do this example. Imagine-- so this is a stack. The operation of putting something into a stack is called pushing. So I do s.push(1). That means, I put a plate with the label 1 in my stack of plates. If I push 9 now, I'll put a 9 in here. I push 3, I'll put a 3 in here.

So the operation of putting something in a stack is push. The operation of getting something out is called pop. Pop does two things. It gives you back an item, and it removes that item from the stack. So it changes the stack. It gives you something, and it changes the stack.

So if I do s.pop, stack.pot means, give me the item that's on the top of the stack of stuff. So the top of the stack here is 3. So stack.pop is taking the top plate off. So we take off plate 3, and that's gone from my stack.

If I do stack.pop again, take another thing off the stack, I'll get number 9. If I push minus 2, I can do that. I'll get a minus 2. If I do pop now, I'll get minus 2. If I do pop again, I'll get 1. If I do pop one more time, I'll get an error.

OK, you got the idea of a stack? It's just like-- in Python, they're implemented as lists. But the idea is that you do these operations always on the same end.

OK, you can look at that if you want to. A queue is different. A queue is meant to be like people standing in line. Some lines are more orderly than others, but this is meant to be like people standing in line. But it involves pushing still.

OK, so we have two operations, push and pop, but they're going to behave a little bit differently. So I push 1 into the queue, so the first guy arrives in the queue. And then, I push 9 into the queue. So far it looks the same. Number 9 arrives. I push 3 into the queue-- excellent.

But now, it's time to serve someone from the queue. If I'm serving someone from the queue, I'm not going-- if I pop the queue, I'm not going to get 3. I should pop the guy who arrived first, right? So if I pop the queue, I'll get a 1. And if I pop again, I'll get 9. And if I pushed minus 2, minus 2 will go here. If I pop, I'll get 3, and so on.

So this is a really useful idea-- stack and queue. They both have the same operations-- push and pop. Now stack is sometimes called a LIFO-- Last In, First Out-- First In, First Out, thank you-- a momentary choke here. No, LIFO-- no, that was right. Last In, First Out.

This one's easier to think about-- First In, First Out. First come, first served-- the first guy who came in is the first one who comes out. Here, it was the last guy to come in who's the first one who comes out.

So if you want to sound like a computer geek from the '70s, then be sure to say, I'm going to put it in a FIFO. We don't talk like that now.

OK, so now that we know about stacks and queues, we can think about how to do depth-first search in Python. And remember in Python, already we had the search algorithm that was just a little bit ambiguous about how it was going to do some operations. And now we can make it totally concrete.

So if we're going to do depth-first search, we're going to use a stack. Remember when we did depth-first search, we were doing all these operations on the same end of our agenda, right? So our agenda is going to be a stack. And when we make a new search node, we're going to do the push operation into the agenda. And we want to get a new node out to expand. We're going to do the pop operation on the agenda.

So agenda is the stack. We put something in using push, and we get something out using pop. And that will have that depth-first search behavior that we saw, OK?

Here's the coolest thing in town. To convert between breadth-first search and depth-first search, the only thing I have to do is change this line of code. In depth-first search, we had a stack. In breadth-first search, we have a queue. Beyond that, it's all the same. We're pushing and popping onto the agenda. It's just that the agenda manages things differently in the two different cases.

So in breadth-first search, we take things off of one end and we put them on the other end. And that's what makes that difference. So it seems kind of cool algorithmically, I think.

OK, so what we have now is a nice algorithm for basically enumerating all the paths. Or, at least, enumerating all the paths in some order until we get to one that reaches the goal, with no particular promise that we will get to one that reaches the goal. But maybe we will.

So this algorithm is sort of like the algorithm I held up at the beginning as the stupidest possible algorithm. So what we're going to do now is spend a little time thinking about how it is that we could avoid even constructing some of those paths that aren't going to be useful to us. So that's the goal now.

So far, we've thought about this abstract tree, which has all the possible paths of length three, and all possible paths of length four, and so on and so forth. But that's kind of too much to think about. So now the question is, well, how many of these nodes can we just totally obviously ignore? So which of these nodes are completely useless?

Rather than trying to count them, somebody just give tell me the name of a path in this tree, or a node, that's useless. Yeah.

STUDENT: ABAB.

PROFESSOR LESLIE KAELBLING: ABAB-- and that's useless. We already talked about this, right? If I'm trying to get from A to somewhere, it might be reasonable to go from A to B. Is it ever useful to go from A to B to A again, if you're trying to get somewhere from A? No, it's not. So any path that goes back to a state a second time is useless. It's never going to be part of a good answer.

So what we're going to ask ourselves as we're building this tree is, could this path that I'm thinking about ever be part of a good answer? And if the answer's no, then we should just ditch it right now, right? Kill it and all of its descendents. We don't care about them. No, not just the parent, but the whole tree.

OK, so here we go. Red states-- we're going to get rid of them. OK, so the red states are on paths that return to a previously visited state. OK, so here we go. A-- that was good. AB-- no problem. ABA-- meh, we don't like ABA, right? Because that returns to a state that it had previously visited. So it can't be part of a nice, short path to somewhere.

So we can go through here and just remove all the paths and their descendants that involve a repeated node-- all paths that involve a repeated state, excuse me. OK, so we can prune out a whole bunch of them.

So we'll call this Pruning Rule 1. We're going to develop some pruning rules here. Don't consider any path that visits the same state twice. So applying that pruning rule, already we go from a pretty big tree to a significantly smaller tree. So that's good. OK, Pruning Rule 1 make sense to everybody?

Now, we're going to talk about it as a pruning rule, but in fact, it's not like we're going to make this whole enormous tree and then go at it with the shears and take parts out. In fact, what we're going to do is just keep in our head that some of these things aren't useful. And we're going to arrange to just really not create them.

OK, so how do we implement pruning rule in our code? Well, so what we've done is, we've got down here, and we've picked a node out of the agenda-- that's the parent node. And we've figured out a state that we can get to from that node. And we looked to see if we got to the goal. If we did, we're happy and we finish.

But now we're going to ask ourselves, is the new state already in the parent's path? Is this new state already in the rest of the path back up to the tree, up to the root? And if it is, we don't do anything. We just say, oh well, this guy's no good. And I don't want his children either. Is that a question or a pose? It's a pose, OK.

OK, so if we ever arrive at a situation where we hit a state, and that state is in our path up to the root, then we just throw that node away, pretend that we didn't see.

OK, so that will have this nice effect of getting rid of all that part of the tree for us. OK, let's skip that. There's another pruning rule. It comes up in some domains and not in others. But if you ever have a situation where you have different actions that take you to the same state, then you should only consider one of them. That's a simple one.

OK, so now let's think about what happens now with that pruning in depth-first search. So imagine here we have the same little grid domain. We do depth-first search. How does it go? We say, from A, we could go to AB and AD. This is actually now our code running. It's code that you'll have to play with.

So we're going to put AB and AD on the agenda. So here, we see the agenda. It's a stack. In this case, we take out AD. I guess we're taking things out from the right. We take out AD, and we're going to add ABE and ADG-- oh, that looks for all the world like a bug. How could that be? Mm, that should be ADE and ADG. ADE and ADG-- how did we get a bug in the output of Python? I have no idea.

OK, good, so we're going to keep expending to the right. And we're going to end up with this path. It goes from A to D to G to H to I, and it visits seven states. So A to D to E to H to I-- that's actually a pretty good path, right? All right, so that worked out pretty well.

So what could we say about depth-first in general as an algorithm? So first of all, if we don't apply Pruning Rule 1, it's a terrible idea, right? Without Pruning Rule 1, we saw that we could go ABABABAB forever-- not a good idea. So it might run forever if the domain is infinite.