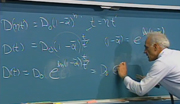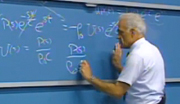Amar G. Bose: 6.312 Lecture 18

DR. AMAR G. BOSE: One of the gentleman who's involved in the videotaping outside just was speaking to me about Bell Telephone Laboratories, and some relationship that they had come up with respect to the spectrum that you hear. Well, this suddenly reminded me of something I probably should have brought up to you, and I was reminded afterward by one of the teaching assistants who had been in the class that's very pertinent to the work we did on transmission lines.

Namely, when they laid the first transatlantic cable, they put a signal in one end and nothing came out the other end. And there was a big to-do about this, as to why. Cable wasn't broken, they knew. And there were all sorts of theories were put forth as to what was going on. And they finally concluded that you needed more capacitance across the line at each end. And they put more and more and more capacitance across the line, and then got no output still. And there was a chap in England named Heaviside, whom I think you've heard of. And he had fallen in some ill repute with the mathematicians of the time, because he dared to deal with things like discontinuities and step functions and whatnot. And he was actually having a hard time publishing papers in any respected journals, but he was a very billion fellow.

And he published somewhere-- I don't remember where it was-- but he published an analysis of this cable as a transmission line. And in electromagnetics, the z0, instead of being rho 0 c, is a root of l/c. And he showed that what you really needed to do was to take the line and open it every so often, and put an inductor in series, all the way across the Atlantic.

And of course everybody-- well, not of course, but everybody said, oh, this is absolutely stupid. He's up to the same old tricks. I mean, my god. Why would you ever put it-- if you're not getting anything out the other end, why would you ever put an impedance in series with this line? It was bound to make it worse, you know?

And so nothing worked. And so finally, Bell modeled this thing up. And to be sure-- I mean, in those days a model consisted of-- you'd make it on a bench. And to be sure, it worked. And so the cable was brought up in all these different points, and inductors were put in, and it worked, and still does.

And so what happened was Norbert Weiner learned of this, and many years later-- I don't remember when. It was maybe in '50s or something-- he wrote a book. He wrote a number of novels, by the way, under a name that is-- I don't remember it, but it's a twist on his own name. But he wrote a novel which, I think it was called, if I'm not mistaken, The Tempter.

And it was a one-to-one correspondence with the events of that line and the people involved. What had happened was Bell Telephone Labs got a hold of an immigrant engineer, a European immigrant engineer, named Pupin. And they named these coils after Pupin. They became Pupin Coils. And Bell Telephone Labs would often patent things this way, under their own people.

And Weiner had quite a social conscience, and he was really disgusted with this whole thing. So he wrote this novel which had a one-to-one correspondence with the people in Bell Telephone and the people in the novel. And it became very well-- I mean, all the people in the engineering at the time knew of this situation, and they made the exact one-to-one correspondence, and there was a very difficult period there where there was tough relations between Bell Telephone Labs and MIT as a result of this novel. But this just shows you what can happen, and some good analysis, just what we now think of as simple transmission line analysis was able to do in a major, major project like that.

By the way, same thing happened to Weiner. The first time network synthesis was ever used in electrical engineering was on a thesis here of Y. W. Lee, who happened also to be a doctorate student of Weiner, and then later came on the faculty. And Lee told me of the situation, that Weiner had not only the first concept of synthesis, but he had a general method which really enables you to synthesize any transfer function you wish that is realizable.

For those in math, it's a series involving Laguerre functions. And so Lee in Electrical Engineering did his thesis for Wiener, and after he finally understood all the math, he then tried some examples. And every example he tried, failed. The Weiner Theory wouldn't work.

So he went to Weiner, and he told him-- he said, look, something must be wrong with your theory. He said, I'm not a mathematician, but everything I try doesn't work. And so Weiner took a look at it, and in his characteristic way-- just looked at it for a few minutes, and then he said, go look up the paper, a recent paper in England, such and such a journal by Hilbert, and I think that'll solve your problem.

Well, it took Lee a year to work over that paper of Hilbert to really understand it. And that's where Hilbert transforms came into electrical engineering, which relate the real and imaginary parts of impedances. And that was a first, also.

When it came time for Lee to present his thesis-- in those days, there were about 23 members on the faculty, and all of them appeared for a doctorate exam. And when Lee came to the part about the real and imaginary parts being related, all the big guns of Electrical Engineering in academia were present, and they jumped on him. They really jumped on him. They said, this was nonsense. Even [? Gilman ?] was present as a young man, but people very experienced like Vannevar Bush. And Lee was just a few years out of China, and a very cultured Chinese family he came from, and he'd never even bounced on like that in his life, and he began to wither.

And they just basically told him, all this was nonsense, and there is no relationship between real and imaginary parts, and we can always change one without the other, et cetera, et cetera. And Norbert Weiner, who is a young fellow there--he's in his early 30s, I think-- was sitting in the group, because he was the thesis supervisor. And when he saw Lee completely collapse, basically-- he had said nothing until this time-- he rose and he said, "Gentleman, I suggest that you all take this thesis home and study it. You will find it is correct."

And that ended the entire meeting, just like that. I mean, everybody knew who Norbert Weiner was, even though he was much younger than all the rest of them. And he just said one sentence, or two sentences, I guess it was, ended the meeting, and they all went home with the thesis, and two weeks later, Lee got a note in the mail-- said, you've passed. They didn't have the decency to say, my God, it's a spectacular job, you know? But I thought you'd be interested in some of the history of how some real firsts took place.

And interestingly enough, here's a first in Electrical Engineering. First time synthesis was ever used, first time Hilbert transforms were brought into it, and which are much more significant than people even appreciate many times today. And it was way back, 1929.

OK. Better get started. What were we going to talk about. Permanent magnets.

In physics, you have seen curves of B versus H that are looking like this for a magnetic material-- all materials to some extent are like that, but usually don't have a big area. These materials are such that if they were in a demagnetized state and you started off, and you applied an H field to it, in other words, you might, if you had a material like that, you might come along and put some steel here and a big coil here, and NI cross it. And you drive an H-field through this.

Well, as you would do that, you'd start here, and what would happen is it would come up in a curve, something like this, and then the bigger the H you put across here, you would get only a little bit of more B. In fact, the amount of B you would get is the same as if it was air. The slope of this would be mu 0 B over H at this point. The incremental slope, or the slope at that point.

And then if you started to take away this field, reduce the current in the coil to 0, it wouldn't trace back down here. It would trace up here. You have so-called hysteresis. And in order to get the B-field down to 0, you actually have to put a reverse current in there-- this is NI-- and bring it all the way down here.

Have you ever witnessed the experiment with a coil wrapped around this magnet while it's getting magnetized and put to a loudspeaker while you slowly crank up the current here? How many have heard such an experiment? Nobody? Well, if you listen to it, it's very interesting. It leaves you with an intuitive picture, right or wrong, of what's going on.

Namely, if you put this coil around here, and then amplify it, and play it on headsets or a loudspeaker, and then just slowly turn up the current, what you'll here is click click click click. All these little domains as they're shifting around in the iron, each one generates a voltage in this coil. And so you hear a whole series of these click click click click click click click, and when you get H-field up over here, then there's many, many less clicks per increment in current.

And then the same thing happens when you start taking away the H-field. You hear some of them start clicking coming down, and when you put the reverse one on. So the actual flipping of those domains which you can also see by putting, [? think ?] powder and whatnot on the surface, you can experience. Well, these materials play an enormous role in engineering, in all forms. And we want to know how to design structures, we can get the basis of how to design a structure with a permanent magnet in it.

Permanent magnets differ from a piece of steel, ordinary cold rolled steel, only in the width of this thing. I mean, everything has this to a certain extent. Steel may have a very high mu, but it has a tiny hysteresis to it, when squeezed down in this fashion. A permanent magnet, as we normally think of it, has a much bigger one.

So we want to get a feel for how you design systems like this. And it turns out, it's very important. Because the biggest cost in most structures that involve motors-- and a loudspeaker certainly is a motor, it's a linear motor-- biggest cost is the magnet. And if you don't understand how to design that, you cannot come up with a minimum cost to do the specified job. And in fact, it's most interesting-- you often will find products on the market in which you take one look at it and you say, oh my god. They had no idea of a few simple laws when they designed this thing.

Now, you don't normally find that in a loudspeaker, because the companies that make the magnetic materials have done it for everybody. They have a table-- if you want to make a four-inch loudspeaker, you do this, and here's the dimensions, and we sell you the material. So the people who use it don't have to know about it. But the minute you want to do something different, i.e. creative, you better understand it.

So let's take a look. Let's grab about the simplest system we can get here to illustrate the principles. This is going to be the magnet material. What I'm drawing, these long arms, are just the, we'll say, steel. And I'm going to make this problem as simple as I can, just so that we get the essence of it. You can put in any additional parameters with ease after that. I'm going to say that this has a mu of infinity, so that its reluctance is 0. The steel parts above. Just makes the calculations a little simpler, but the concept is the same.

We're going to say that this is what you want, in here. In other words, you may be doing a physics experiment. You want a certain B field in here. Let's call that the-- I'll give an arbitrary sign to it. However it comes out, we'll see. We'll call that B sub gap. We have here an area of the gap. We have a length of the gap. And we'll of course have an H in the gap. I have no idea, before I put any constraints down, which way these Hs and Bs are going to go. We'll have here, let's say, a B of the magnet, an H of the magnet, a length of the magnet, and an area of the magnet.

Now, the object of the game is, given this, as you would normally be given it-- if it's a physics experiment, you would be given the dimensions of the gap, because whatever you want to put in there is going to determine that. And you'd be given the B field that you need. Which of course by B gap, as you know, in the air, B gap is mu 0 times H gap.

So this would all be given by the people who want to use it. Your job is to produce the machine that has that gap with that field, and the minimum size magnet that will do the job.

Well, let's see. Yes, we already finished magnetic circuits. So let's apply KCL and KVL. KCL, if I made a node up here, this is all one big node, if you wish. Its mu is infinite. I'd write B sub magnet times H magnet. Sorry-- B sub magnet area magnet. B times area is the flux going into that node. And this flux is coming out. So I would write B gap area gap equals 0. That's KCL. Some of the flux is going in as 0.

KVL? Well, KVL, remember some of the magnetomotive forces around a closed loop, integral hl dl, or H summation H sub l in the discrete case, h sub l times l? So I would have H magnet times l magnet-- I'll just take them around clockwise. So they're both going the same way in the signs that I've defined, plus H gap l gap is equal to 0. And that's KVL.

Now, it's going to be-- what the heck? Well, this one's down about-- all right. It's going to be amazing-- I'm going to have to keep these now. Because how much information we will get out of just these two equations? Now let's just multiply. We'll take these over to the other side, the two terms-- let me do it-- and then I'll multiply both sides. B sub m A sub m is equal to B sub g A sub g. H sub m l sub m is equal to minus H of g L sub g.

Now, this equation, first one, the KCL, implies that if let's say B sub m is greater than 0 if B sub gap is greater than 0, clearly. The areas are positive numbers, and if this is positive, then this is positive. This equation says, H sub m is less than 0 if H magnet is greater than zero.

Interesting. We'll see this, but it's just interesting that this is going to happen. If H is going down this direction here, this H is going to be negative. And don't get scared, because it's possible to have a positive B and a negative H also, with the VI relation, if you wish, of that element, the Bh relation of that element.

OK. But now let's multiply the left sides and the right sides. B sub magnet times H sub magnet times a magnet-- let's see. Wait a minute. Yes. Area magnet l magnet. That's the left sides multiplied together. And the right sides multiplied together-- the minus sign B sub gap, H sub gap, a gap, l gap.

Now, this fellow here is the volume of the magnet. This is the volume of the gap. So finally, we get B sub magnet H sub magnet times the volume of the magnet equals minus B sub gap H sub gap of volume of the gap. Now, B sub gap H sub gap BH. This is air here, so I can replace this by what? H is B over mu 0. So in this case, I can say minus B gap squared over mu 0 times B gap.

Now, just from these two simple equations we, already have an answer for what is the minimum volume of the magnet. Everything over here is given. All of this. This is to be determined.

Now what I want is the smallest volume of the magnet. Why do I want the smallest volume? Because you pay per gram of this stuff, and you want to minimize the cost. And then-- yes?

SPEAKER 1: If you [UNINTELLIGIBLE] use this magnet by, I don't know how, putting something in the gap or something, wouldn't that invalidate these equations that are [UNINTELLIGIBLE]?

DR. AMAR G. BOSE: Yeah. That's a good question. I mean, if what you were going to put in the gap that you'd have to know that, if what you were going to put into the gap was a great big slug of metal, of steel, let's say, that took up an appreciable part of the gap, then everything would change. Normally when you design something like that, it's sort of like, let's say, taking a big battery, a car battery, and saying, I'm going to do some experiments with transistor circuits, low-power transistor circuits.

You know the voltage isn't going to change. So you would design this thing, knowing what experiment you want that what you did in here wasn't going to change the basic reluctance of the gap. So your B was going to be B all the time. In truth, if you put something little, in there, yeah, it does change B, but it doesn't change it very much.

Now, if you took the magnitude-- let's take the magnitude of both sides of this. B sub m, H sub m, V sub m is equal to the magnitude of this, which is Bg squared over mu 0 Vg. If this is all given, the minimum volume occurs when the product of B and H in the magnet is max. The product is given-- do you want this small? You make whatever's left in the product very large. Maximize this fellow.

Now, to maximize him, you go over and you look at your BH curve for the magnet, and you say, well, where on that BH curve is-- this is the material now. B for the magnet and H magnet. I know that, by the way, I'm going to be at negative H. I already found that out from looking at the Kirchhoff Laws.

So over in here, where am I going to get the maximum magnitude of the product? Well, if I took the product of B times H and plotted it, B is 0 here, B sub m. So the product must be 0. H is 0 here, so the product must be 0. And as I go between these two points somewhere along here, the curve will peak. The product-- this is the product of B sub magnet, H sub magnet. 0 at these two points, because H is 0 or B is 0, and it has some magnitude of the over here.

Now, that's the point that we will call B o-- too many letters we're getting down here, but optimum, opt. And H optimum. B magnet optimum H magnet optimum.

So we now know that we will get the minimum value of volume of the magnet, if I arrange it somehow that when this thing is all done and delivered to you, that B and H inside of that magnet have the values given off by that curve. How we can do that is another story. We'll have to worry about that. But as long as I rearrange it so that when delivered to you in the final form, B and H are given by this point here, we're in. Smallest magnet will do the job.

By the way, there's something else that's very interesting here. It comes right out of the equation that's on the board. I don't know whether to write another one, if it makes it confusing or not. But let me rewrite this equation here, the one up there, and write it as-- well, no, I won't rewrite it.

In electromagnetics, just like in electric circuits, as you know, you found out that the energy or power was V times I, and energy in electromagnetics was 1/2 B times H. So this is within a factor of 2. The total energy density was BH, 1/2. But within a factor two, this is the energy of the magnet, the total magnetic energy, when it's operating anywhere that it says here, even without the optimum.

This or this is the magnetic energy in the gap. So when you have something that has a mu of infinite over here, the total magnetic energy of the magnet appears in the gap. And that's why the energy of the magnet is so important.

SPEAKER 2: What about the right side of the graph? How do you know it's the maximum [UNINTELLIGIBLE PHRASE] where that point is?

DR. AMAR G. BOSE: Yeah, I don't care, because I know that my solution for this is going to be for H magnet less than 0. And we'll talk about that in a minute. But you can see it right out of the Kirchhoff Laws. So that's why I looked only over here. Because in truth, you have one in each quadrant.

So very important to realize that in a magnetic structure, where you would design it properly not to have much loss in here, NMF drop in here, that the energy in the magnet appears in the gap. And so when you talk about motor design, or talk about linear motors, any kind of motors, transducers of any sort that use magnets, you talk about the energy of the magnet.

Now what we'd like to do is just go one step beyond, and find out what is the length on the magnet, and what is the area. We now know that somehow if we rearrange this, we're in. Well, if we arrange that, what is the length of the magnet? What is the area of the magnet?

Back to our simple, simple, simple Kirchhoff Laws. It is amazing, by the way, how people can come away from something in this field looking like it's very complicated and you had so many relations to get things, but they all come out of the same thing. So I will assume that I have B magnet equal to the optimum, H magnet equal to H optimum. Haven't said how I got there yet, but let's assume I get there. Because I'm going to get there, and when I get there, I want to know what the size of my magnet is going to be.

So let's just look at KCL. B magnet optimum, which I now know, times A magnet, the area of the magnet, equals B gap-- well, I just take it that way, if we want. B gap A gap. So B mag, this implies, then, that area of the magnet-- because this is known, area of the gap. That was given to you. The field that you wanted in the gap was given to you. You now know B optimum. So A is simply B gap A gap over A magnet. So we have that one.

To find the length of the magnet, just go to KVL. Same story. H of the magnet, L of the magnet, H of magnet optimum, l magnet is equal to what? H gap l gap. Or if you want to still go back to B is equal to B gap over A gap, which is known-- whoops. B gap over mu 0 times l ga, all of which are known. And therefore, H magnet is equal to B gap-- let's see. Just a moment.

SPEAKER 3: [INAUDIBLE]

DR. AMAR G. BOSE: Wait a minute. What did I do here? Hold on a second. Yeah, I want to find-- yeah, that's all right. I want to find out the length of the magnet. Yeah, sorry. l magnet is equal to B gap l gap over mu 0 times l times H. Jeez, what have I done? Let's see. Solve for this fellow. I want to put the H down here, B up here-- yeah. H magnet optimum.

OK. We have-- oh, and the equation above, B gap, A gap-- yeah. Optimum.

SPEAKER 2: A and B gap.

DR. AMAR G. BOSE: Yeah. B gap BM-- hold it-- optimum. Don't confuse me. I'm confused enough already. OK.

Now this magnet, turns out-- I heard somebody say, haven't you lost a minus sign? And the minus sign, if I got away with it, I would have lost it, but I clearly didn't. Somebody said it's in there. And so this gives a negative length.

Now, one of the things that you should keep in mind is that magnet material with negative length is very, very expensive. And so this is a good way to remember that this fellow is going to be with a minus sign on him.

We have obtained the result we wanted. We have a minimum volume magnet whose volume you can compute, because you have A of the magnet and you have l of the magnet. Best use of the magnet, exactly what we wanted to determine. Turns out there's a lot more to learn about permanent magnets, and there's a very interesting thing. Let me ask and see if you know the answer first. It won't be so exciting if you do. But if you don't, it's fascinating, at least for me.

Let's suppose you're going to build some sort of a motor, and it's going to have a permanent magnet in it. And I now ask you as an engineer, well, when are you going to magnetize this thing? Obviously you buy the materials, it's not magnetized. Now, you're going to magnetize the magnet, and put the materials, and then build the thing, or are you going to build it and then magnetize it? You could build this magnet into a big complicated structure, can choose to magnetize that whole structure, or you could choose to magnetize a magnet and assemble the structure.

How many would say that you would magnetize the magnet first? All right. How many would say that you would wait until the whole structure was built and magnetize the magnet? Oh boy. It's almost all equal. Hm. Well, I guess you do it either way you want, then. It's about equal vote.

Let's find out which way. You don't have a choice, it turns out. You do have a choice, but you would make a miserable design one way and good design the other way. Not a design. A good product. The product's already designed. One way it'll come out as we designed, and the other way, it will not.

Let's go back and look at Kirchhoff's Voltage Law and Kirchhoff's Current Law again for this, but instead of expressing it this way, I'll express it in terms of fluxes and reluctances. Flux in the magnet. That's the first term in the upper left here. B times A. If I took this over to the other side, which I hope I did somewhere. Yeah, here. Flux in the magnet is equal to flux in the gap. That was KCL.

The other statement was that the sum of the drops of the MMF around a closed loop is 0. Sum of the drops is 0. So H from the bottom equation, the MMF of the magnet is equal to-- take it over to the right hand side-- minus MMF of the gap. Two basic evasions.

Now, I can plot curves for-- well, the easiest one. Let's plot a flux MMF curve for, let's say, the gap. Flux gap MMF. MMF gap. Flux in the gap, MMF in the gap is a straight line. And it's flux in the gap, MMF gap, what's the slope of that line? Anybody know? It's the first of the three Ohms Laws. The gap. Current is MMF. Flux current is voltage divided by resistance, only it's a fancy R in this thing. So slope of this line is 1, then, over the reluctance of the gap.

That's a nice simple one. Now let's try to do it for the other one. Namely for the magnet. Now, flux, that's just like [? BEA, ?] except it has an area in it. And this is just like H, except it has a length in it. H times l is MMF. H times i, if it's a source, is MMF.

So let's plot the flux in the magnet as a function MMF for the magnet. That's just like the BH curve. Looks, is shaped something like this. It's a scale factor on each axis, a little bit different.

Now, it's still supposed to be symmetrical. I joined them a little bit nicer than they normally look, but. OK.

And then what does this set of equations say? You've all obviously had things load lines on transistors. If you put a resistor across the output, you know how you might have had for a bipolar, a current versus voltage. And you put the load line across, and you find out where you're operating. Well, all of that just fell right at a KCL and KVL, if you remember. That's exactly what happens. Again, you don't have much else to depend on here.

So KCL says flux is equal MMF minus at equilibrium. So what do I do? Well, let's plot one of these things with the MMF reversed. That's all we do. Take either one you want and flip it around. If I flip this one, for example, around here, then I have a graph of phi, the same way, except against minus MMF. So we flip it around here. Looks like this. And here, then-- this is the slope now-- equal to minus 1 over reluctance of the gap.

So in order to get the magnet material to be at the right operating point, you pick the reluctance such that the 1/Rg falls right through here. It's a graphical way of looking at it. And this point being defined as the point for where-- this is not a BH curve, but it's where B is optimum. B magnet opt corresponds to this point. H magnet optimum.

OK. Now iron has another property, this permanent magnet has. And that is, if we bring--- we're just now ideally dealing with this material, which we can control the H field in, from something external, like I said, a big coil here, which has-- that's the magnet material. I have a big coil here so I can drive H to whatever I want. That's a bad color.

It turns out there's something else you learned, I think, in physics, about these curves. Just like if you started from 0 and you went up here-- I mean, you don't go out here and up here. this curve has history to it, anything that has hysteresis. And if you start it here, you go up like this, and you come down-- well, if you came down here, for example, which means that you had the magnet fully saturated. You're now cutting back the current. At this point, you're reversing the current. You're pulling the curve down, down, down, down, down. And then at this point, for some reason, you stop. And you say, well, I'm going back up again.

Well, when you go back up again-- you've heard of minor loops that go up like this. This would eventually go back up to here, and once you're back up in there, then of course you would, if you came down all the way, it would cycle here. So these are the so-called minor loops that it goes on. The domains aren't all turned around, and they start turning around, and you start going up.

So now look what happens. If you take this magnet and you say, OK, I'm going to magnetize it and then assemble it. Let's say we do that. So that's the nice thing to do, because the magnet is invariably smaller than the apparatus plus magnet. And if you want to create a big H field across something, remember that whatever you're doing, the energy is all in the darn gap. And so your magnetizer has to develop a tremendous amount of energy if you want to magnetize something that's in the gap this big, as compared to something that's in the gap this big.

So this is the thing you like to do, really, is magnetize the magnet first. Well, if you do that, the minute you turn the magnetizer off, which is this big coil with this thing around it, you go into a reluctance. This magnet now looks out into not the magnetic structure that we drew first, the one with the arms in the gap, but it looks out into space, who has much bigger reluctance and the structure here has. This only has this little air gap to worry about. If I took all this stuff away, oh my god. Now it's looking out into space. So look what happens. You go down to a reluctance like that. This is without the structure. Our reluctance without structure.

And now you say, oh, that's all right. I'll put it together. Now I put on the arms that made that drawing and come to the gap. Well, what happens when I do that, is I start going up here. Where do I intersect the final reluctance? The final reluctance is the reluctance, when it's all assembled, of this path here. Which since this is infinite, this is just a little one here. That's a small reluctance. So that's this one that we wanted, 1/Rg, and now here's where I settle.

So if you magnetize something outside, which is convenient to do, if you magnetize the magnet first and then assembled the thing, you lose, always. So you always want to magnetized the thing first. Makes a huge, huge difference.

Besides that, by the way, I told it was easier to do it the other way. It is. It's easier to do it the other way, but the doggone thing becomes like a rat trap when you try to assemble it. You get these two arms anywhere near, and then, whang! They just is go together. Keep your fingers out of the road. I mean, basically, you would never want to have to assemble. If it didn't go together first the right way, you have a heck of a problem. I mean, it's fortunate that we have to magnetize it afterward, except we have to pay a huge price for the magnet.

On the last day, you will see a-- part of your trip-- if you ask about it, I'm not sure they would think of showing it to you. But on the various assembly lines where transducers are made, you will find the magnetic assembly that magnetizes these things, and you'll see them going along a belt. And all of a sudden, they'll go like that. The magnetic field socks them so badly that the whole darn thing jumps. And it's an incredible field. It's designed by another MIT person with very advanced power processing technology.

And the first ones that we used that he designed-- because the ones available in industry just weren't good enough to do the -- and the first one that he designed, when we would take students through there, we would say, now-- I don't think is true anymore, but you can take a look, it might be-- that you wiped half a cycle or so right out of the AC power line, and the lights would go, oop! Every time the speaker went jump, all the lighting in the building went oop! like this. Because it took so much power, so much energy, so much current that was going into the magnetizer, because you're magnetizing the whole structure now, all at once.

But if you don't get this thing up here-- I'll do it over here. If you don't get this magnet up here, if you only get it up to here, boy, good luck. I mean, you've got a curve that goes down like that. And so your whole device will have much less magnetic field. And you saw, in the case of the loudspeaker, that if you have much less magnetic field, and the speaker were designed to do that, it will do that. Worse. Yeah?

SPEAKER 6: [UNINTELLIGIBLE] if I wanted to magnetize a magnet outside of its composition, if I were to keep it in something whose reluctance is lower than [UNINTELLIGIBLE PHRASE] was able to put it in while maintaining the--

DR. AMAR G. BOSE: Yeah. I got you. The question is, if-- and that's the hook-- if you magnetize it outside, and you were able to maintain it in a structure which was lower, having a smaller reluctance, then you'd come to here, and then you'd drop down to here. But it's a very interesting thing to think about. Suppose you had such a structure. You'd have to get rid of that structure and put the other one on. And how you do that without going through a reluctance that is much larger is a neat trick.

Now just a little bit about magnetic materials. They differ very, very much. The structures that were used, mostly because that was what was available, up through, I would say, certainly through the '50s and partially '60s, was Alnico. And this was a magnet material which had about 10,000 gauss saturation level. And don't remember the H-axis numbers. But I will just draw you with time what has happened to the shape of this curve, and then tell you the consequences of the shape change.

If this was Alnico, then-- well, I'm going to draw other curves on here. I don't want to put the labels on yet to point out where they're going to go. Then there was a change, and we'll see why, to barium ferrite or strontium ferrite, and that curve might look about like this. This is the BH curve we're drawing. Might look about like this. The H curve for the material. And then there comes along another one-- there are several, actually, but neodymium iron, which has even a little bit more than the Alnico up here. And its curve looks like that. No room to finish it. This is neodymium, this is Alnico, and this is, let's say, strontium ferrite.

The looks of those curves, turns out, are having a big effect on magnetic design. The magnetic energy that you can get out of the max BH that's in the strontium ferrite is huge. The peak is somewhere out here. It even has a little bit more maximum B. But you don't care what the B is. I mean, here's one that has the lower B, the strontium ferrite. But it has a bigger H. So you can get maybe a bigger, if I've drawn that correctly, a bigger BH product. That's what you care about in the thing.

Now, the first interesting difference is the following. How many of you know how you demagnetize a magnetic material? Oh, jeez. Only a few. How do you do it?

SPEAKER 7: [UNINTELLIGIBLE] very hot.

DR. AMAR G. BOSE: You can do that. Heat it. But another way? Yeah?

SPEAKER 8: You can, like if you drop a magnet sort of thing? [UNINTELLIGIBLE PHRASE]. Or if you can put a B-field on it in the other direction.

DR. AMAR G. BOSE: Put a B-field on it the other direction? Getting warm. Yeah?

SPEAKER 9: Very high-frequency alternating magnetic field?

DR. AMAR G. BOSE: High frequency alternating magnetic field? There are elements in what you said that are correct. Jeez. You're all born in the digital watch age, I can see. Never were fooling around the laboratory and had your watch get all magnetized. Yeah?

SPEAKER 10: [INAUDIBLE PHRASE].

DR. AMAR G. BOSE: Aha. Put it in an alternating magnetic field. Doesn't have to be fast. 60 hertz will do. And slowly decrease the field.

They sell audio and video bulky erasers-- just a platform that generates a magnetic field. You put the tape on, turn it on, it's 60 hertz, that's all, and then you pull the tape off slowly. If you pull it off-- I played around with it one time, just to see if this is really true. Put on like audiotapes and cassette tapes, and you put them on-- no, I guess they were reels. You put them on, and then go, whish! And you see what's remnant on there. You listen to the music or whatever you had recorded. And it's amazing how much is still there. Put the thing on and go like this, and a little bit of hocus-pocus, and everything is gone.

Basically, what happens is, if you cycle this thing to a little lower limit each time, you keep getting smaller and smaller and smaller. You're bringing it off. If you do it right-- you don't want to stop here or something. You want to go down here, make the hysteresis loops go smaller, smaller, smaller, smaller until you get down to here. And so that's basically how you demagnetize something.

Well, AC signals, to be sure, give the magnet problems. I mean, somebody just said, put it in an AC field. Now, that's not going to do it any good, I'll tell you that. In other words, in terms of preserving wherever you were, if you cycle this thing any way, you're going to wind up somewhere different than this point, and that is bad news.

So look now, let's go back to our loudspeaker model for a second, which is a linear motor. Just so it's very clear, I'll draw-- the tiny little speaker we brought in was an old one with an Alnico magnet sitting down here. This is the structure. Let's call this infinite mu here for the moment. This is the magnet. This is the so-called pole piece, and the voice coil is around here.

Now, this is the same way the flux flows, OK? Around like so. So the coil is exactly where the flux flows through the magnet. And the coil has in it-- guess what? AC. The amplifier's feeding 100 watts into this silly thing here, just pumping right through the magnet. So there's an H all the time that's varying.

Now turns out that with Alnico-- Oh, let me see. Did I mention about the first speaker that we made, that every one was bad after it was on the shelf? Well, it turned out that the last test on the assembly line was a buzz test to see if, when the person put the grille on, if he dropped some staples inside that were going to rattle around. Or if he didn't fasten it firmly enough. So our folks had designed a big 400-watt amplifier, and they went brrrp! right on the loudspeaker, after all the tests. Packaged it all, and put it up in the finished goods.

Well, there's one fellow-- more than one today, I guess-- who were assigned to do nothing but go, every day, up to finished goods, pick out products that are ready to be shipped, pull them down, take them apart, and make all the measurements on them, thank god. Because every single one failed the measurements before it was shipped. The rules are, you sample a few, and if the few indicate a problem, then of course you go to the large number.

Well, every one of them failed. And at first it was a huge mystery. Every one passed all the tests, failed when they were upstairs. And they couldn't find anything special about upstairs. And so they finally realized, oh my god, there was a buzz test. After all the other tests, somebody hooked a 400 watt amplifier on there, and yanked the magnet all around, and it wound up in a different state.

Well, that was all stopped, and this fellow was crossed out. And we went to the strontium ferrite, and that has a much wider H before you're ever going to drag that thing around. In other words, here you don't need much H at all to bring B right down to 0. Here you need a heck of an H to do it.

And so it turns out that if you drop a photograph, in those days, a stylus on a record, that was enough of a transient to shake the BH curve up and wind up at less than B optimum H optimum for the product. Or-- any of you who have owned a hi-fi have no doubt had the experience of pulling the jack out of one of the inputs when it's wide open, and you get one heck of a shock with the sound. Well, the magnet got a heck of a shock in all Alnico speakers, and to this day, there are a heck of a lot of those in homes that are now sounding like the one we drew with the big fundamental resonance, very low bass, and no highs because the Alnico, you could shake around here.

And it was very interesting, because for one or two decades after that, there were companies that were advertising, "We use only Alnico magnets in our loudspeakers, the most expensive magnet"-- actually, it wasn't even expensive. This was more expensive. But the Alnico had a major, major, major problem. So we did not know that when we designed the first product, and we found that out in a very strange way. But now with neodymium, that's another story, totally.

There are some other interesting points that separate the materials. Alnico has a high mu, a high B/H ratio. That's why the curve is thin and tall. And this thing has a very low-- essentially, neodymium has a mu of 1. And that enables you to do interesting things. I'm not going to go quite that far. But you have enough fundamentals do to it now.

In an Alnico structure, if you had a little gap right here, even, you would have a problem. You'd lose a lot of energy in that thing. And the B-field over here would go way down. Also the issue of leakage. The leakage flux differences are very unique. You know, the reason that a magnetic field stays in here, the only reason that it stays in here and doesn't go this way, or doesn't come around here, is because this has less reluctance. Well, if the magnet has a high mu or a low mu, very much determines the fringing field that you have out here. And so you'll see Alnico magnet structures looking like this, to keep this area very, very far away from here, et cetera. And you don't need to do that when you go to the ones with the wider BH curves in them.

Now, something like this material, by the way, there are only a couple of companies in the world that make it at the moment. And it just was 1980 or so that they started developing this. That material costs 100 times per gram what this material costs. However, it has 10 times the energy density that this material has. So small things can be done with this that you would need huge ones for this. Because to get the same energy, you'd need 10 times the volume in this fellow than you do in this.